Exercise 2: Fluxibility and Tvent

Before going into more detail, let’s have a closer into the case we explored last week.

  • Load the homogeneous or layered case with constant

  • Use the paraview calculator to create a new variable T_Celsius (by doing T_Celsius = T - 273.15)

  • Make a z-normal slice

  • And explore the 100,200,300,400,500 °C contours through time?

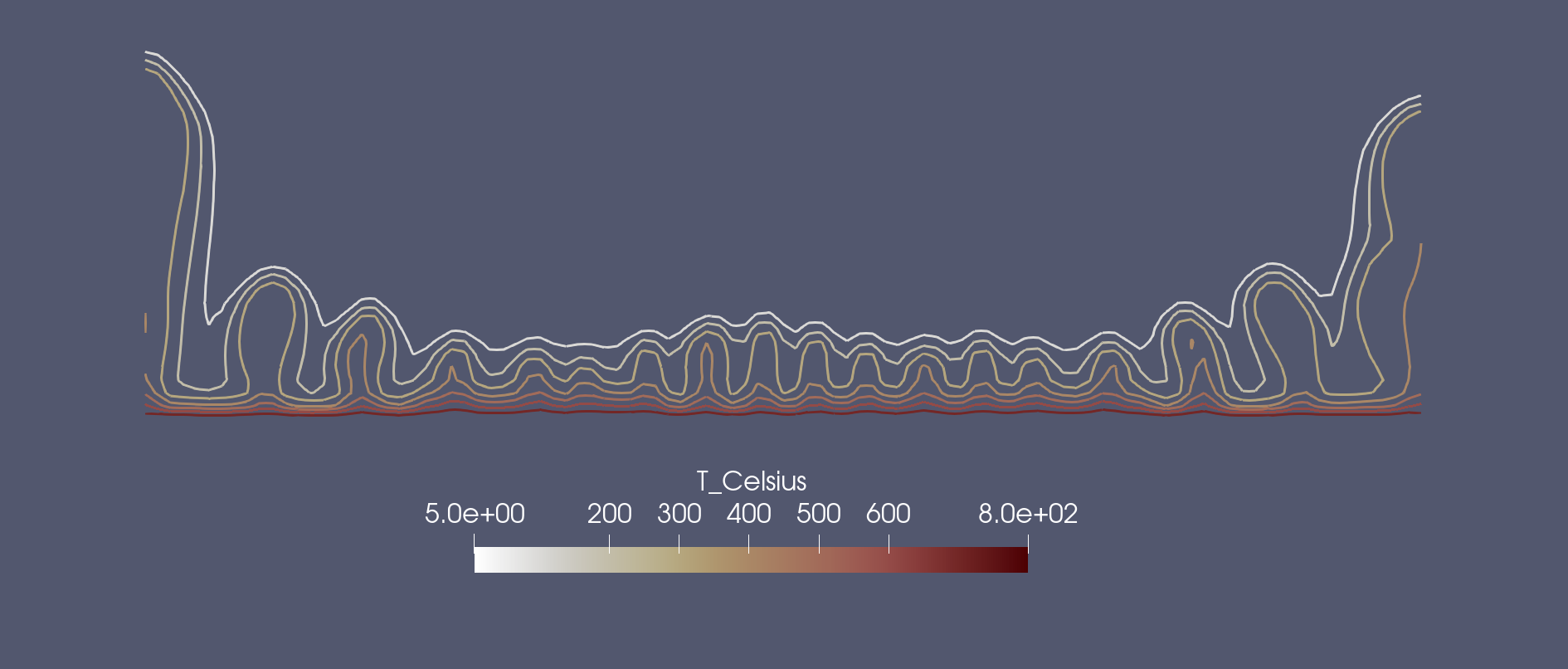
../../_images/Fluxibility_postprocess.png

Fig. 29 Notice how the diffusive thermal boundary layer becomes unstable between the 300°C and 400°C isotherms. This is what concept of fluxibility tells us!

[Jupp & Schultz, 2000] concept of fluxibility was later extended to explore interrelations between permeability on vent temperatures [Driesner, 2010a], the structure of hydrothermal flow zone [Coumou et al., 2008], and fault-controlled off-axis hydrothermal system [Andersen et al., 2015]. Some of these papers are available in the e-learning site of this course for registered CAU students.

Let’s look into the original setup! We will try to reproduce the results presented by [Jupp & Schultz, 2000]. The setup is very similar to the simple single plume driven by a gaussian heat source we had simulated previously.

Model setup and running the case

We are simulating a 3700 x 1000m sized box with a gaussian constant temperature boundary condition at the bottom. The general model setup is shown in the Figure below. The OpenFoam case can be downloaded from here: Jupp_Schultz.

(Source code, svg, pdf)

../../_images/Exercise2-1.svg

Download the case file, unzip it and copy it into your shared folder that is accessible both from your local system and from the docker container. Check out the usual files like system/blockMeshDict, run.sh, 0/T. Make sure you understand the setup!

Code modifications and local Rayleigh number

We have learned about “fluxibility” but let’s go one step back and first think about the vigor of convection in general. The tendency of a fluid to convect and the vigor/regime of free convection is often expressed by a dimensionless number, the famous Rayleigh number, \(Ra\). It naturally shows up as the driving force of convection, when the governing equations are non-dimensionalized, or one can follow a more classic derivation. There is a good explanation on wikipedia .

Formally \(Ra\) is the ratio between the time scales of heat transport by diffusion and convection.

Let’s have a quick look and do a quick dimensional analysis. Simple heat diffusion looks like this:

(32)\[\frac{\partial T}{\partial t} = \kappa \frac{\partial^2 T}{\partial x^2}\]

Let’s make the variables dimensionless by introducing characteristic scales:

(33)\[T' = \frac{T}{\Delta T}\]
(34)\[x' = \frac{x}{L}\]
(35)\[t' = \frac{t}{\frac{L^2}{\kappa}}\]

There we have it. The characteristic time of diffusion is \(\tau_{diff} =\frac{L^2}{\kappa}\) with units of \(s\).

Alright, let’s look at convection. In Darcy flow the velocity is proportional to the density difference according to \(u \sim \frac{\Delta \rho g k}{\mu}\). If we express the density difference via the thermal expansion and divide the characteristic length, \(L\) by this velocity, we get \(\tau_{conv} =\frac{L \mu}{\Delta T \alpha \rho g k}\), which again has units of \(s\).

So the Rayleigh number is:

(36)\[Ra = \frac{\frac{L^2}{\kappa}}{\frac{L \mu}{\Delta T \alpha \rho g k}}\]
(38)\[Ra = \lvert \frac{\rho \Delta T \alpha g k L}{\kappa \mu} \rvert\]

With this analysis in mind, we probably expect that the local Rayleigh number is highest, where also the fluxibility is high. The Rayleigh number derived above is a measure for the vigor of convection in the entire domain. We can follow [Jupp & Schultz, 2000] and derive a local Rayleigh number by relating convective and diffusive fluxes:

(38)\[Ra_L = \lvert \frac{\nabla \cdot (\vec{u} \rho h)}{\lambda \nabla^2 T} \rvert\]

The convective energy transport, \(\nabla \cdot (\vec{u} \rho h)\) term is back! If you read [Jupp & Schultz, 2000] carefully, you find a dimensional analysis that shows that \(Ra_L\) becomes maximum where that transport term is maximum and we are back to the fluxibility concept.

Enough theory, let’s put this into a model. The compute local Rayleigh numbers, we have to add something to the code. There is a dynamic code section within system/conrolDict that allows outputting more variables including the thermodynamic properties of water. Look how easy it is to evaluate the local convective and diffusive fluxes.

 1functions
 2{
 3    calPlumeT
 4    {
 5        libs                ("libutilityFunctionObjects.so");
 6        type                coded;
 7        enabled             true;
 8        writeControl        adjustableRunTime;
 9        writeInterval       $writeInterval;
10        name                plumeTemperature;
11        codeWrite
12        #{
13            //get maximum tempeature on the top boundary
14            label patchID = mesh().boundaryMesh().findPatchID("top");
15            const volScalarField& T = mesh().lookupObject<volScalarField>("T");
16            const volScalarField& mu = mesh().lookupObject<volScalarField>("mu");
17            const volScalarField& Cp = mesh().lookupObject<volScalarField>("Cp");
18            const volScalarField& rho = mesh().lookupObject<volScalarField>("rho");
19            const surfaceScalarField& phi = mesh().lookupObject<surfaceScalarField>("phi");
20            const volScalarField& h = mesh().lookupObject<volScalarField>("enthalpy");
21            double kr = 2.0;
22            // calculate local Rayleigh number
23            volScalarField Ra_L("LocalRayleigh",mag(fvc::div(phi, h) / (kr*fvc::laplacian(T))));
24            // write properties to output files
25            mu.write(); Cp.write(); h.write(); Ra_L.write();
26            // write vent temperature
27            std::ofstream fout("ventT.txt",std::ofstream::app);
28            // Info<<"Plume Temperature: "<<mesh().time().value()/31536000<<"\t"<<Foam::gMax(T.boundaryField()[patchID])-273.15<<" C"<<endl;
29            fout<<mesh().time().value()/31536000<<"\t"<<Foam::gMax(T.boundaryField()[patchID])-273.15<<std::endl;
30            fout.close();
31        #};
32    }
33}

Update hydrothermalFoam

Some early version of HydrothermalFoam did not have access to the specific enthalpy. If you get an error due to this, you can easily update to the latest version. Go into the docker container shell and

cd $HOME
./getHydrothermalFoam_latest.sh

This will update the source code of HydrothermalFoam and recompile it. Just wait for it to complete. Now you can run the case!

It’s possible that we have been a bit overambitious in our chosen numerical resolution. In case the run-time is too long, just reduce the horizontal and vertical resolution. Make the mesh with blockMesh and call the solver; or execute the run.sh script. If you are feeling courages today, you can also try our running it in parallel! Check out the run_par.sh script for that. You can also shorten the total run-time (to say 40 yrs) in system/controlDict; we are mainly interested in the early stages anyway.

Post-processing

Plotting temperature

After running the case, check it out in paraview and make sure you understand the results and that everything looks fine. While paraview is great for 3-D processing, sometimes python can be more powerfull in detailed post-processing.

The figure below shows an example plot of the final temperature solution. It basically does the same thing as paraview, but let’s walk through it.

../../_images/T_Jupp_Schultz_steady.svg

Fig. 30 The steady-state temperature distribution. See Temperature + velocity field (quiver) in the notebook.

Click on the link in the figure caption and go through the notebook. Safest way of getting this to work is to copy the steps into local notebooks (see Installation guide).

You can also start up paraview and explore everything there! Check which temperature contours become unstable first, plot vectors and local Rayleigh numbers.