Script for calculating steady state 1D advection-diffusion using FDM methods

import numpy as np
import numpy.matlib
from scipy.linalg import solve
from scipy.sparse import spdiags
import matplotlib.pyplot as plt
from matplotlib import animation
from IPython.display import HTML
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300

# model parameters
c       = 20
k       = 2
nx      = 11
x0      = 0
x1      = 1

Tleft   = 0
Tright  = 1

X,dx    = np.linspace(x0,x1, nx, retstep=True)

#peclet number for stability analysis
peclet  = c*dx/(2*k)

#analytical solution with boundary conditions T(0) = 0 and T(1) = 1;
C2      = 1/(1-np.exp(c/k))
C1      = -C2;
Tana    = C1*np.exp(c/k*X) + C2

# hide: the code in this cell is hidden by the author

## FTCS solution
## build the coefficient matrix
#data  = (np.ones((nx,1))*np.array([???, ???, ??? ])).T
#diags = np.array([-1, 0, 1])
#A     = spdiags(data, diags, nx, nx).toarray()

## and add boundary conditions
#A[0,0]       = 1
#A[0,1]       = 0
#A[nx-1,nx-1] = 1
#A[nx-1,nx-2] = 0
#Rhs          = np.zeros(nx)
#Rhs[0]       = Tleft
#Rhs[-1]       = Tright
#Tftcs=solve(A,Rhs)

# hide: the code in this cell is hidden by the author

## upwind solution
## build the coefficient matrix
#data  = (np.ones((nx,1))*np.array([???, ???,  -???])).T
#diags = np.array([-1, 0, 1])
#A     = spdiags(data, diags, nx, nx).toarray()

## and add boundary conditions
#A[0,0]       = 1
#A[0,1]       = 0
#A[nx-1,nx-1] = 1
#A[nx-1,nx-2] = 0
#Tuw=solve(A,Rhs)

# plot everything

fig = plt.figure(figsize=(10,5))
fig.clf()
ax  = plt.axes(xlim=(x0, x1), ylim=(Tleft, Tright))
line, = ax.plot([], [], lw=1)
ax.set_xlabel('Distance')
ax.set_ylabel('Temperature')
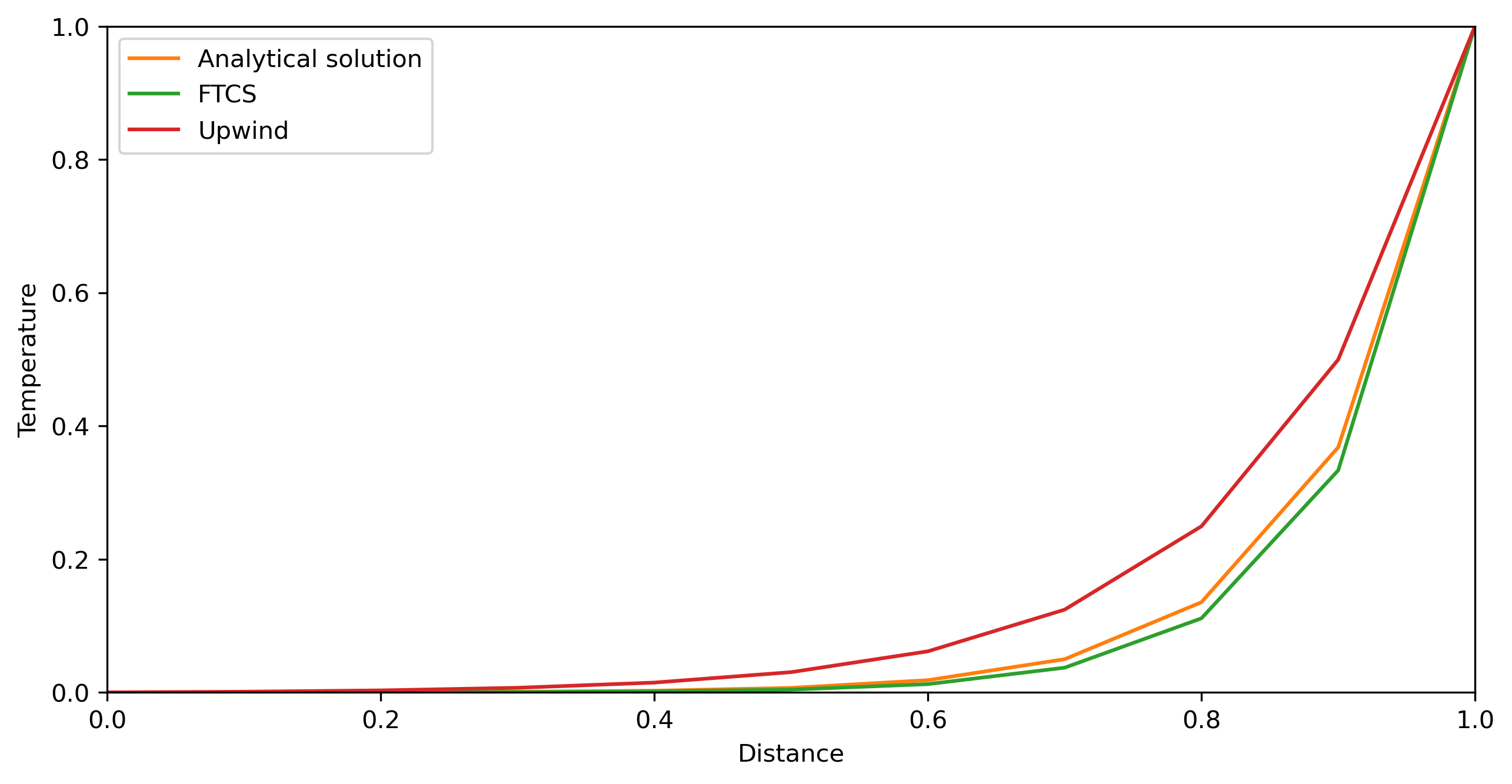
plt.plot(X, Tana, label='Analytical solution')
plt.plot(X, Tftcs, label='FTCS')
plt.plot(X, Tuw, label='Upwind')

plt.legend()

plt.show

<function matplotlib.pyplot.show(close=None, block=None)>