MWR example problems¶
[33]:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
from sympy import *
Analytical solution¶
[37]:
c_vec = np.array([1,5,20]) # velocities
K = 1 # diffusion constant
nx = 100 # grid points
x0 = 0 # left boundary
x1 = 1 # right boundary
# make the mesh and the grid spacing
X = np.linspace(x0,x1, nx)
[38]:
# function to compute analytical solution with boundary conditions u(0) = 0 and u(1) = 1
def solve_analytical():
C2 = 1/(1-np.exp(c/K))
C1 = -C2
u_ex = C1*np.exp(c/K*X) + C2
return u_ex
[39]:
# Plotting
fig = plt.figure(figsize=(10,5))
fig.clf()
ax = plt.axes(xlim=(0, 1), ylim=(0, 1))
line, = ax.plot([], [], lw=1)
ax.set_xlabel('Distance')
ax.set_ylabel('Function value')
# compute solutions
for c in c_vec:
u_ex = solve_analytical()
plt.plot(X, u_ex, label='Analytical solution c = %2i K = %2i' %(c,K))
plt.legend()
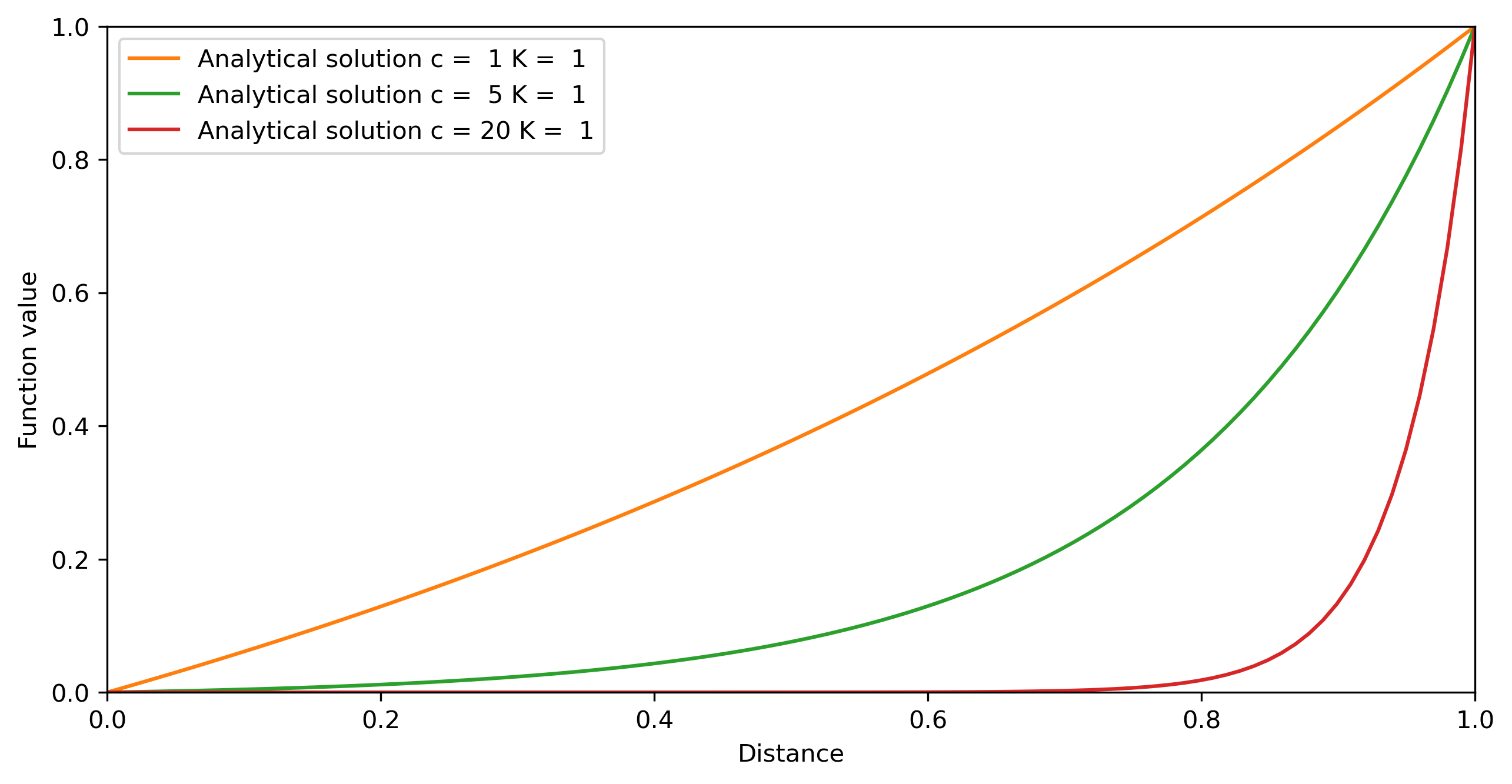
Weighted residual results¶
[66]:
# global variables
K = 1
c = 5
# analytical solution
C2 = 1/(1-np.exp(c/K))
C1 = -C2
u_ex = C1*np.exp(c/K*X) + C2
[67]:
# collocation method
a2 = symbols('a2')
xc = 0.5 #collocation point
Ri = c*((1-a2)+2*a2*xc) - K*2*a2
a2 = solve(Ri, a2)
a2 = float(list(a2)[0].n()) # convert result to float
a0 = 0 # boundary conditions - see the script for details
a1 = 1-a2 # boundary conditions
# so that the final polynomial is
u_c = a0 + a1*X + a2*(np.square(X))
#check of the solution -> first derivative - second derivative at x=0.5 needs to be zero
print(c*(a1 + 2*xc*a2) - K*2*a2)
#compute the RMS error
E_rms_collo = sqrt(np.sum(np.square(u_ex - u_c))/nx)
E_x_collo = np.sqrt(np.square(u_ex - u_c)/nx)
0.0
[68]:
# hide: the code in this cell is hidden by the author
[69]:
# least squares
#a2,x = symbols('a2 x')
#Ri = ??? #definition of residual
#Wi = diff(Ri,a2) #weight function is derivative of R with a2
#a2 = ??? #symbolic solution
#a2 = float(list(a2)[0].n()) # convert result to float
#a1 = 1-a2;
#a0 = 0
#u_ls = a0 + a1*X + a2*(np.square(X))
#compute the RMS error
#E_rms_ls = sqrt(np.sum(np.square(u_ex - u_ls))/nx)
#E_x_ls = np.sqrt(np.square(u_ex - u_ls)/nx)
[70]:
# hide: the code in this cell is hidden by the author
[71]:
# Galerkin
#a2,x = symbols('a2 x')
#Ri = ??? #definition of residual
#Wi = ??? #weight function is derivative of R with a2
#a2 = ??? #symbolic solution
#a2 = float(list(a2)[0].n()) # convert result to float
#a1 = 1-a2;
#a0 = 0
#u_g = a0 + a1*X + a2*(np.square(X))
#compute the RMS error
#E_rms_g = sqrt(np.sum(np.square(u_ex - u_g))/nx)
#E_x_g = np.sqrt(np.square(u_ex - u_g)/nx)
[72]:
# plotting
fig2, (ax1, ax2) = plt.subplots(2, 1, figsize=(10,7.5))
# prepare axis
# function value
ax1.set_xlim(0, 1)
ax1.set_ylim(0, 1)
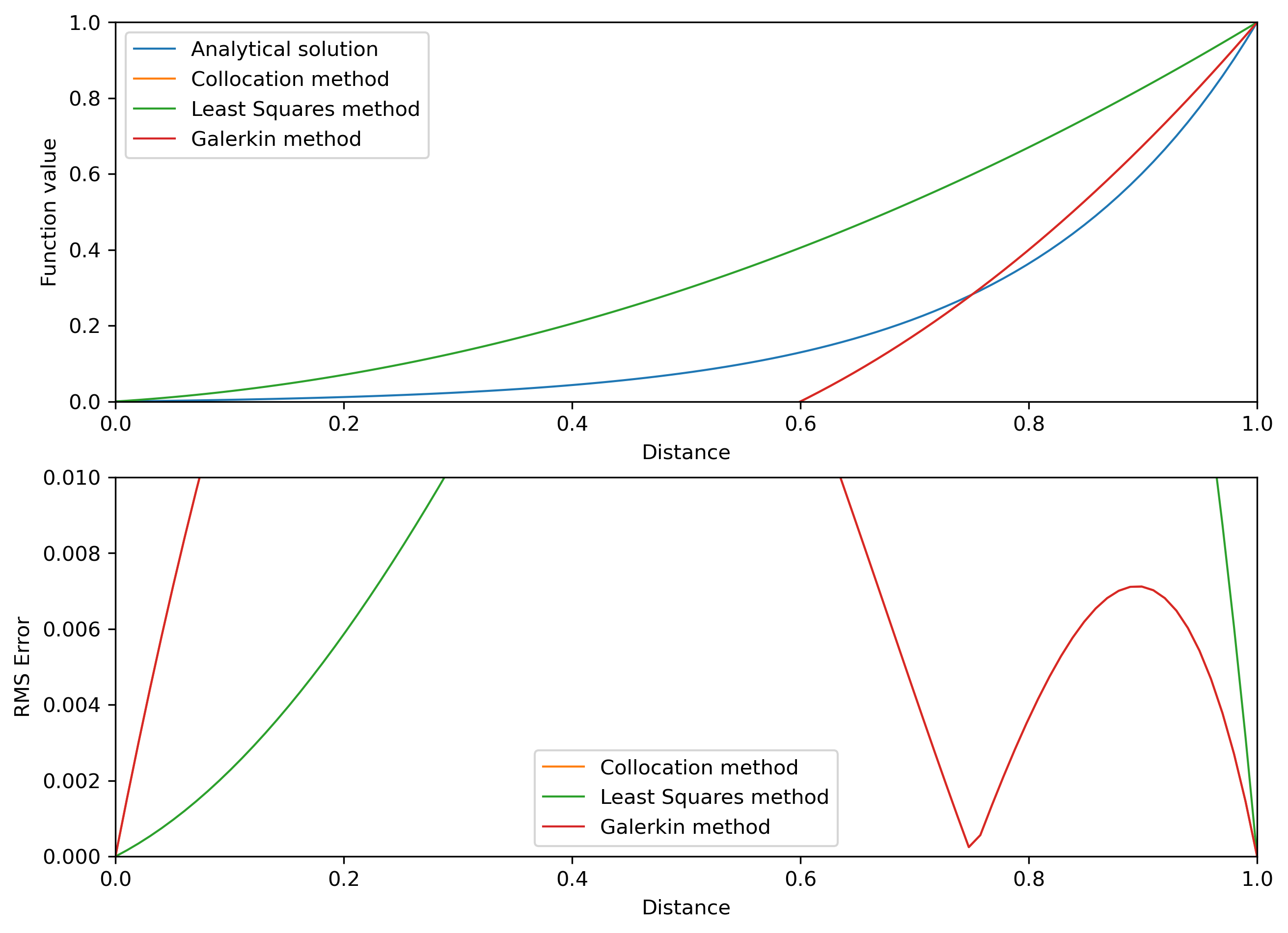
ax1.plot(X, u_ex, lw=1, label='Analytical solution')
ax1.plot(X, u_c, lw=1, label='Collocation method')
ax1.plot(X, u_ls, lw=1, label='Least Squares method')
ax1.plot(X, u_g, lw=1, label='Galerkin method')
ax1.legend()
ax1.set_xlabel('Distance')
ax1.set_ylabel('Function value')
# error estimate
ax2.set_xlim(0, 1)
ax2.set_ylim(0, 0.01)
ax2.plot([],[],lw=1)
ax2.plot(X, E_x_collo, lw=1, label='Collocation method')
ax2.plot(X, E_x_ls, lw=1, label='Least Squares method')
ax2.plot(X, E_x_g, lw=1, label='Galerkin method')
ax2.legend()
ax2.set_xlabel('Distance')
ax2.set_ylabel('RMS Error')
[72]:
Text(0, 0.5, 'RMS Error')
[ ]:
[ ]: