Upflow temperatures in submarine hydrothermal systems

A striking observations from global vent fluid measurements is that fluid exit temperatures apparently never exceed 400°C (Fig. 17 ).

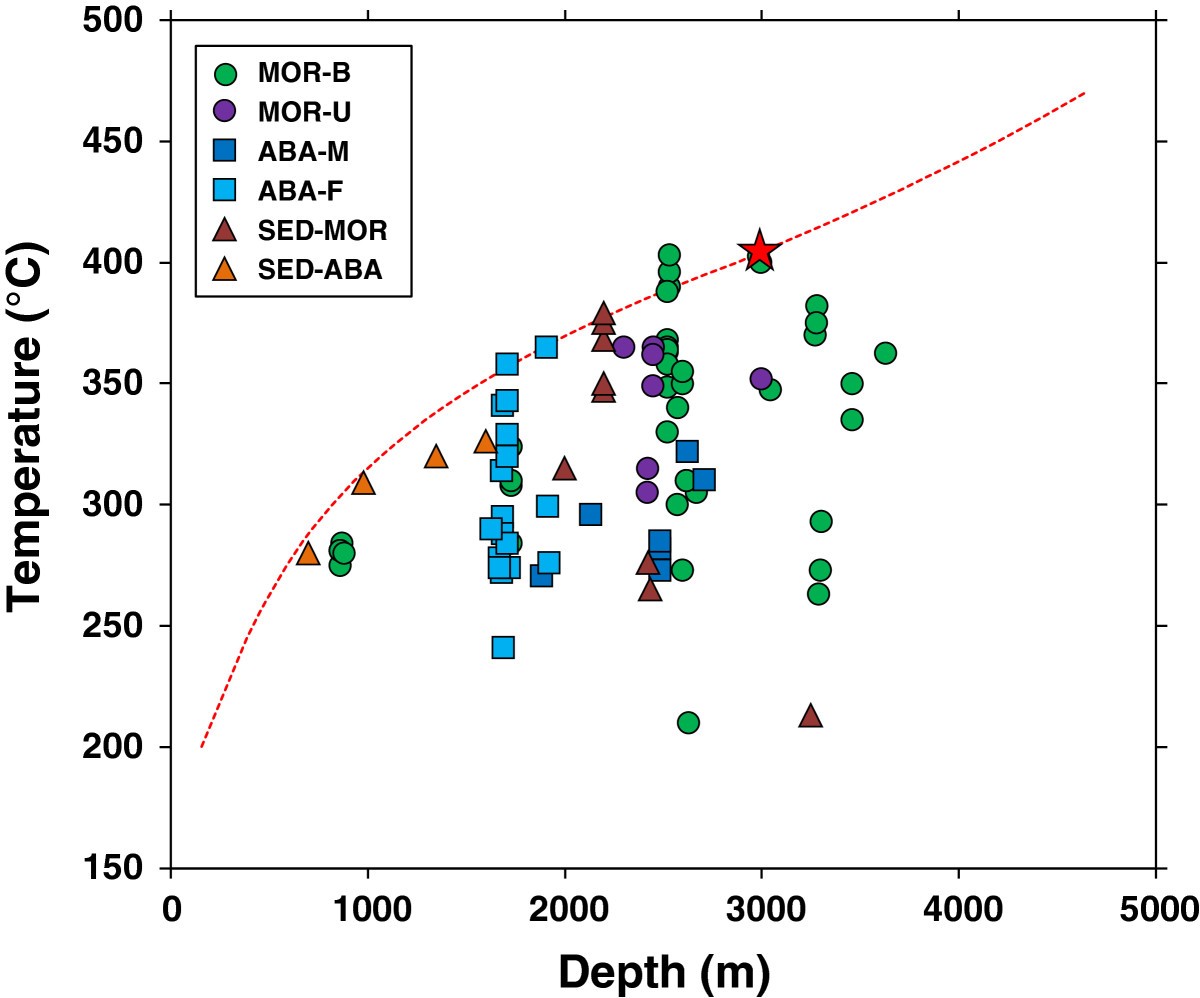
Fig. 17 Figure taken from [Nakamura & Takai, 2014] showing measured vent fluid temperatures.

Maybe you have already noticed in our convection experiments in the previous session that the upflow temperatures are always much lower than the bottom boundary condition implying that the hottest fluids are actually stagnant and do not rise towards the seafloor. [Jupp & Schultz, 2000] published a landmark paper in which they showed that the thermodynamic properties of water control the upflow temperature and can explain the observed upper limit of vent fluid temperatures. In this lecture we will have a detailed look into the proposed mechanisms.

Mechanism to limit black smoker temperature

We recommend reading the original papers by [Jupp & Schultz, 2000] and [Jupp & Schultz, 2004]; here we only provide a very short summarry. The underlying idea is to determine from the pure water equation-of-state the optimum temperature for buoyant upwelling. Within the energy conservation equation, advective heat transport is described by a divergence term:

(23)\[\nabla \cdot (\rho h \vec{U})\]

Following [Jupp & Schultz, 2000], we can assume that the pressure gradient, driving upflow, can be approximated as cold hydrostatic so that we can express the upflow velocity as:

(24)\[U_z = \frac{k}{\mu} \left( \nabla P - \rho g_z \right) \approx \frac{k}{\mu}(\rho_0 g_z - \rho g_z) = g_z \frac{k}{\mu} (\rho_0 - \rho)\]

Now we plug this expression into equation (23) to get:

(25)\[\nabla \cdot (\rho h \vec{U}) = \frac{\partial}{\partial z} \left(\frac{(\rho_0 - \rho) \rho h}{\mu}\right) g_z k\]

[Jupp & Schultz, 2000] called the term wihtin the large brackets, \(F=\left(\frac{(\rho_0 - \rho) \rho h}{\mu}\right)\) , fluxibility. Fluxibility is a function of fluid properties only and those properties are pressure and temperature dependent. To first order, advective heat transport is maximized, where \(\nabla \cdot F\) is maximum and this divergence can be approximated within the basal boundary as \(\nabla \cdot F \approx \frac{\partial}{\partial z} F \approx \frac{\partial}{\partial T} F\) .

Fig. 18 a shows fluxibility as a function of pressure and temperature. It is clear that this function has a distinct peak at temperature of approximately 400°C. Fig. 18 b shows sections of constant pressure and also the derivative of F with temperature. The peaks in these functions mark the temperature for which buoyant heat transport is most efficient for a given pressure. Later we will explore this further in numerical convection experiments.

Fig. 18 Fluxibility F as a function of temperature and pressure (a), profile of F along temperature with constant pressure (b).