FD calculation of radioactive decay
We will solve for radioactive using explicit and implicit FD schemes.
Load libraries and set resolution of output figures
[1]:
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['figure.dpi']= 300
Define physics constants, here we use arbitrary values without any physical meaning
[2]:
c0 = 1 # initial concentration
k = 0.1 # decay constant
Setup numerics
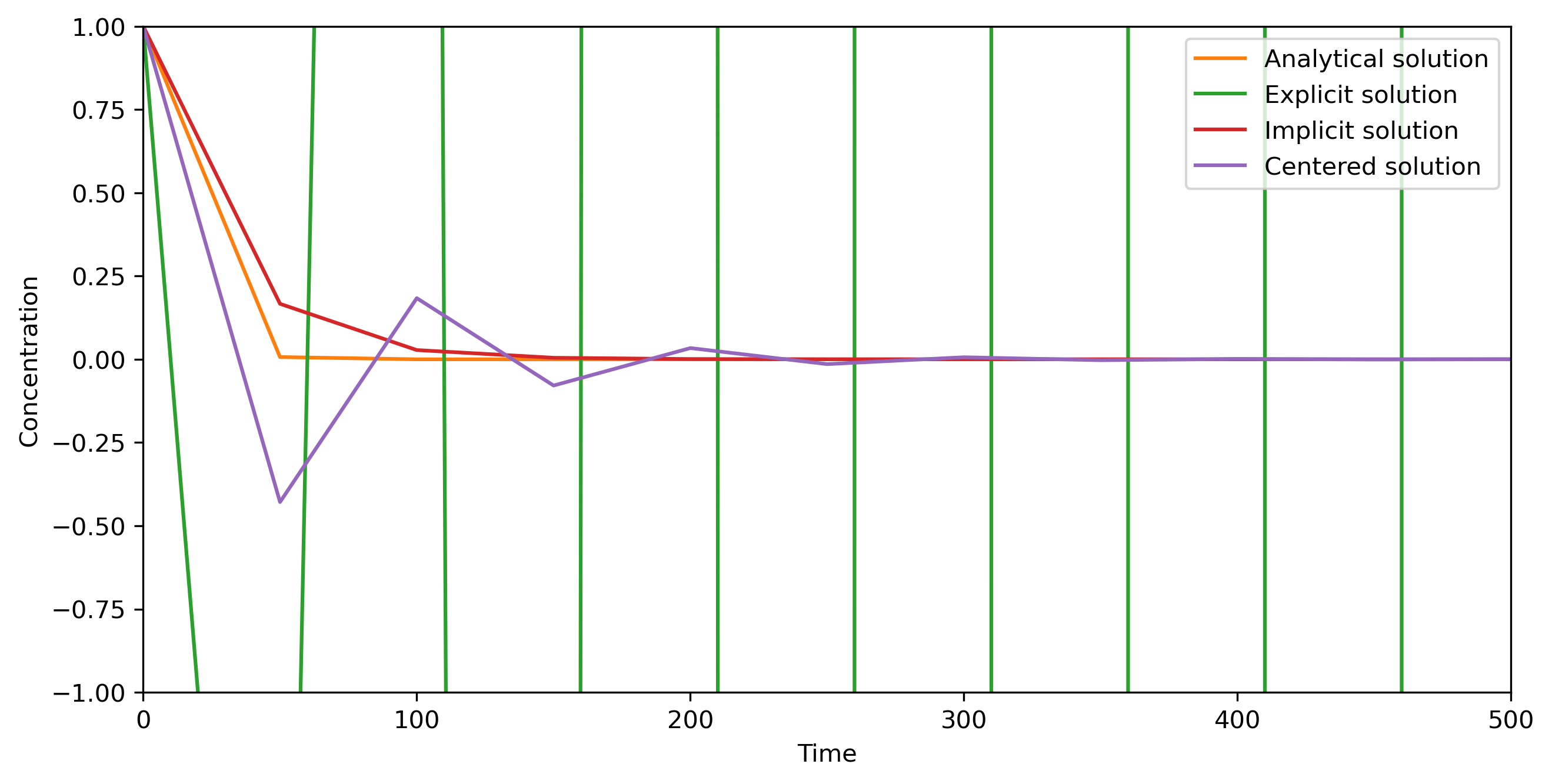
[69]:
dt = 50 # time step
steps = 11 # number of time steps
Cana = np.zeros(steps) # analytical solution
Cana[0] = c0 # initial condition
Cexp = Cana.copy() # make a copy
Cimp = Cana.copy()
Ccen = Cana.copy()
Time = np.linspace(0, (steps-1)*dt, steps) # time stepping, and Time vector
Perform calculation
[70]:
# hide
for n in range(0,len(Cana)-1):
Cana[n+1] = np.exp(-k*Time[n+1]) #analytical
Cexp[n+1] = Cexp[n]*(1-k*dt) #explicit
Cimp[n+1] = Cimp[n]/(1+k*dt) #implicit
Ccen[n+1] = Ccen[n]*(1-k*dt*0.5)/(1+k*dt*0.5) #centered
[71]:
# write update rules for the explicit and implicit cases!
# Bonus: write an update rule that uses the concentration at the middle of the time step
#for n in range(0,len(Cana)-1):
# Cana[n+1] = np.exp(-k*Time[n+1]) #analytical
# Cexp[n+1] = ???
# Cimp[n+1] = ???
Plot different solutions
[72]:
# First set up the figure, the axis, and the plot element we want to animate
fig = plt.figure(figsize=(10,5))
fig.clf()
ax = plt.axes(xlim=(0, dt*(steps-1)), ylim=(-c0, c0))
line, = ax.plot([], [], lw=1)
ax.set_xlabel('Time')
ax.set_ylabel('Concentration')
plt.plot(Time, Cana, label='Analytical solution')
plt.plot(Time, Cexp, label='Explicit solution')
plt.plot(Time, Cimp, label='Implicit solution')
plt.plot(Time, Ccen, label='Centered solution')
plt.legend()
plt.show
[72]:
<function matplotlib.pyplot.show(close=None, block=None)>
[ ]:
[ ]: